Welcome to our group
We are the Statistical Physics Group at the Faculty of Mathematics and Physics, University of Ljubljana, working in the field of statistical and many-body physics. Our research spans a broad range of non-equilibrium phenomena in classical and quantum systems. We use analytical and numerical methods for exploring universal laws of complex behavior in many-body systems.

Research
Transport in low-dimensional systems
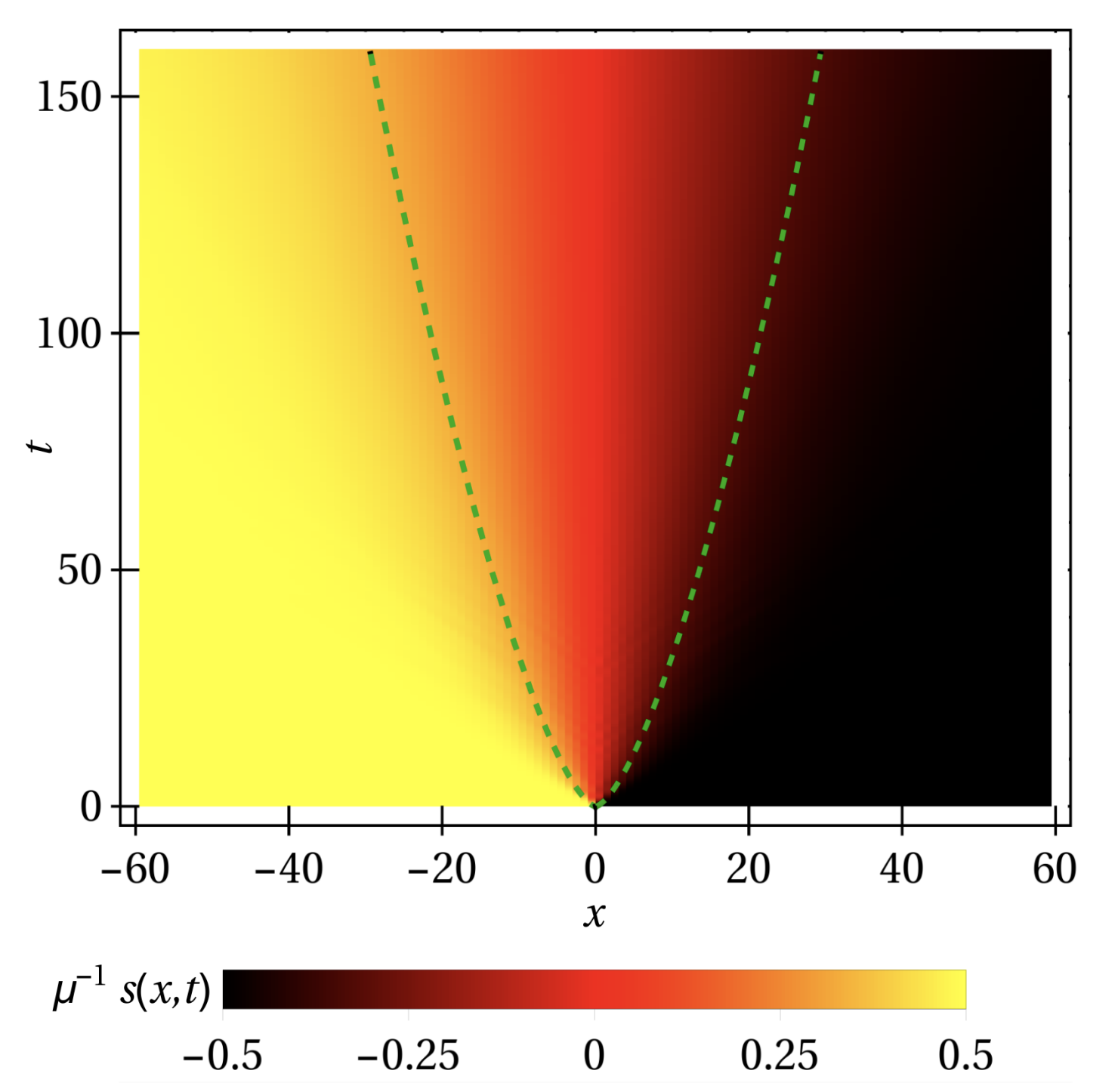
Understanding how conserved quantities propagate in interacting systems is a central problem of non-equilibrium many-body physics. In low-dimensional settings, transport can be strongly constrained by symmetries, in particular in integrable models with extensive sets of conserved quantities. Beyond conventional ballistic or diffusive transport, such systems can exhibit anomalous behaviour such as superdiffusion, subdiffusion, or diffusion with non-Gaussian fluctuations.
By combining exact results, numerical simulations, and hydrodynamic descriptions, we aim to identify microscopic mechanisms that underlie different transport behaviors.
Selected publications:
- Families of quasi-local conservation laws and quantum spin transport
T. Prosen, E. Ilievski – Phys. Rev. Lett. (2013) - Kardar-Parisi-Zhang Physics in the Quantum Heisenberg Magnet
M. Ljubotina, M. Žnidarič, T. Prosen – Phys. Rev. Lett. (2019) - Absence of normal fluctuations in an integrable magnet
Ž. Krajnik, E. Ilievski, T. Prosen – Phys. Rev. Lett. (2022)
Open many-body quantum systems
Coupling a quantum many-body system to an external environment can give rise to fundamentally new behavior that has no counterpart in equilibrium settings. At long times, such systems relax to a non-equilibrium steady state, which may carry persistent currents and interesting correlations.
We study steady states of driven and dissipative systems to uncover new non-equilibrium phases. This gives us insights into the intrinsic properties of the closed system itself, such as its transport characteristics.
Selected publications:
- Third quantization: a general method to solve master equations for quadratic open Fermi systems. T. Prosen – New J. Phys. (2008)
- Matrix product simulations of non-equilibrium steady states of quantum spin chains. T. Prosen, M. Žnidarič – J. Stat. Mech.(2009)
- Non-equilibrium phase transition in a periodically driven XY spin chain.
T. Prosen, E. Ilievski – Phys. Rev. Lett. (2011)
Quantum many-body chaos
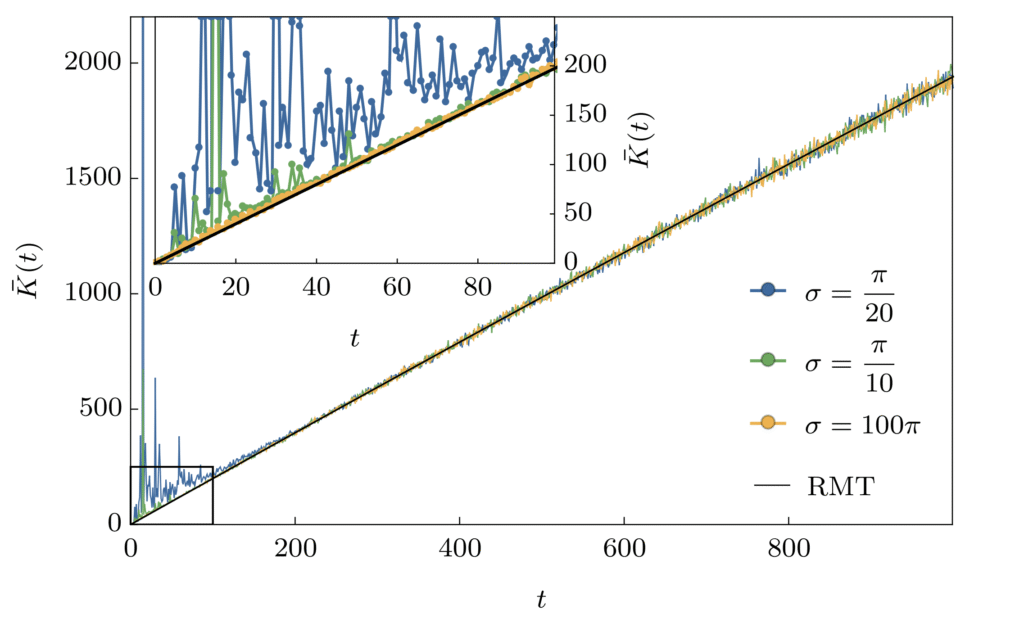
Classical chaos is characterized by exponential divergence of trajectories. On the other hand, quantum systems display chaos through universal properties in the statistics of energy levels.
We focus on studying and developing probes of chaos in different quantum settings, such as quantum spin chains and open quantum systems, as well as on constructing minimal models that allow for analytical access to chaos diagnostics.
Selected publications:
- Exact Spectral Form Factor in a Minimal Model of Many-Body Quantum Chaos
B. Bertini, P. Kos, T. Prosen – Phys. Rev. Lett. (2018) - Complex Spacing Ratios: A Signature of Dissipative Quantum Chaos
L. Sá, P. Ribeiro, T. Prosen – Phys. Rev. X (2020) - Ruelle-Pollicott resonances in quantum systems
T. Prosen – J. Phys. A (2002); M.Žnidarič -Phys. Rev. E (2024)
Our Tools
Integrability
The presence of an extensive set of conservation laws in integrable systems leads not only to rich and unconventional physical phenomena, but also provides powerful analytical tools to study many-body dynamics. In our group, we use integrability techniques, such as the Bethe ansatz and the inverse scattering method, to gain analytical insight into the properties of interacting many-body systems.
See for more details:
- How Algebraic Bethe Ansatz works for integrable model
L. Faddeev – arXiv (1996) - Introduction to Classical Integrable Systems
O. Babelon, D. Bernard, M. Talon – Cambridge University Press (2003)
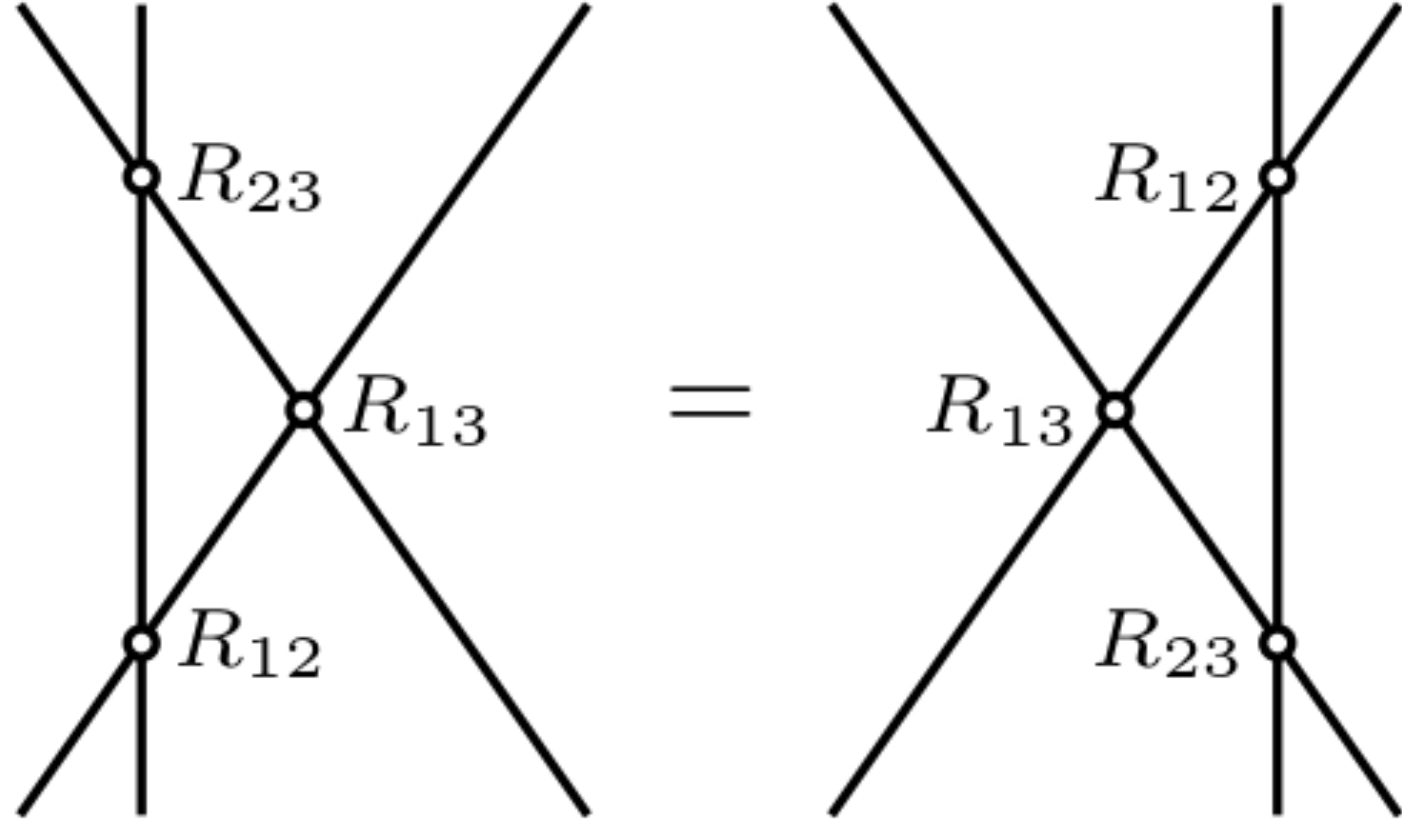
Circuits and tensor networs
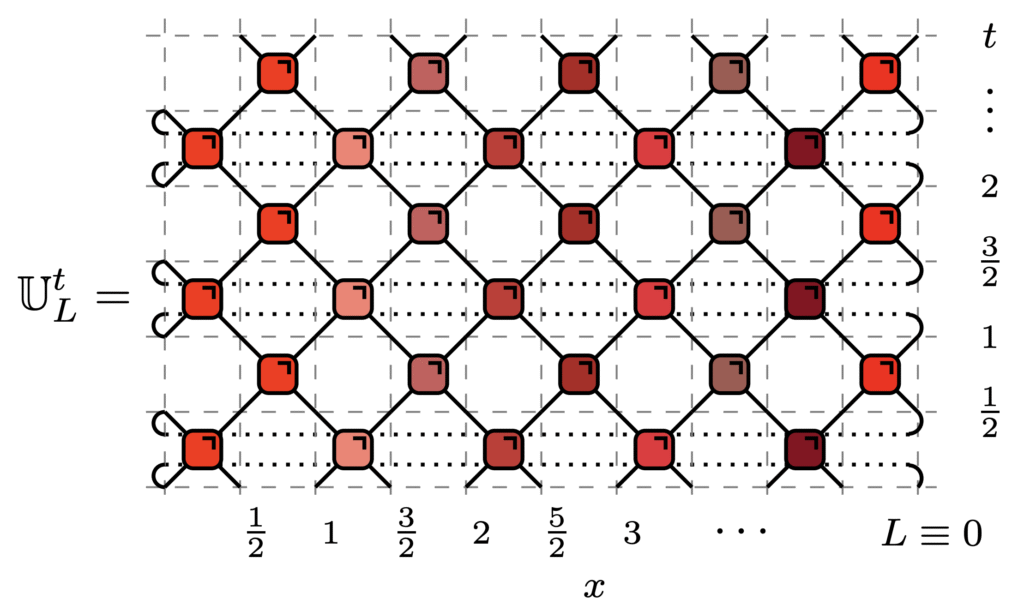
Tensor networks provide a useful framework for studying many-body systems. For instance, by Trotterizing Hamiltonian time evolution, one naturally arrives at efficient numerical algorithms such as TEBD and DMRG, which are based on tensor-network representations like matrix product states. These methods allow us to simulate the dynamics of interacting many-body systems well beyond the reach of exact diagonalization. At the same time, studying quantum circuits ab initio offers a complementary route toward analytical understanding of non-equilibrium many-body dynamics.
See for more details:
- The density-matrix renormalization group in the age of matrix product states
Ulrich Schollwöck – Annals of Physics (2011)- Exactly solvable many-body dynamics from space-time duality
B. Bertini, P. Claeys, T. Prosen – arXiv (2025)
Cellular automata
Cellular automata can be viewed both as a special limit of quantum circuits without entanglement generation and as purely classical dynamical systems with a discrete phase space. Their simplicity allows for large-scale numerical studies of dynamical observables, enabling access to system sizes that are far beyond what is achievable in other many-body setups. At the same time, cellular automata often admit analytical progress, providing valuable insight into the underlying physical mechanisms. By constructing models with update rules that encode essential microscopic interactions, we efficiently analyze their dynamical properties and emergent behavior.
See for more details:
- Rule 54: Exactly solvable model of nonequilibrium statistical mechanics
B. Buča, K. Klobas, T. Prosen – J. Stat. Mech. (2021) - Ergodic behaviors in reversible 3-state cellular automata
R. Sharipov, M. Koterle, S. Grozdanov, T. Prosen – arXiv (2025)
Members
















